Na základní škole nás v hudební výchově učila soudružka učitelka stupnici. Namalovala pět linek, houslový klíč a pak prozpěvovala: “cé, dé, é, ef,” a tak dále, až najednou “ááá”.
“Moment! Slyšel jsem dobře, souško?,” dotázal se a přestal jsem kružítkem vyrypovat do lavice háknkrajc.
Áčkem se vůbec nezačínalo?
Takže mý celoroční úsilí, kdy jsem se nakonec tu abecedu celkem obstojně naučil bylo zcela marný a zbytečný?
Úča nereaguje na můj dotaz, provokativně prozpěvuje dál a stoupá si v lodičkách Púchov na špičky, haleká “háá” až nakonec už vysloveně piští. Prvně jsem myslel, že ji nějaký hlodavec vlez pod sukni, ale pak v tom jekotu rozeznávám zcela zřetelně: “céééééé”.
Cože??
Prý je to nějaké jiné cé než tam to první, dozvídám se, a šmytec.
Fajn. Hudba nemá logiku! Tímhle si hudbu, stupnici i noty zařazuji do škatulky dalších školních podivností, přestává mě zajímat a jdu si radši počítat pythagorejské trojúhelníky.
Za nějaký čas mi mí zlomyslní sourozenci bohužel nakukali, že Albert Einstein, který patřil mezi mé tehdejší vzory společně s cikánem Rumbou, který zase dokázal vydržet půl minuty pod vodou na jedno nadechnutí, tak že prý Albert Einstein hrál na housle!
Chvíli jsem se s touto zradou vyrovnával, ale nakonec jsem tedy začal chodit do houslí k soukromému učiteli hudby, panu Turzovi (čest jeho památce). A tam jsem někdy počal už zcela pochybovat o konzistentnosti světa vůbec. Vysvětlim. Když se začínáte učit na housle, nejprve vás tam naučí takové jakoby údržbářské dovednosti. Jak si napnout šmytec, jak si namazat šmytec kalafunou, jak si nic nevypíchnout šmytcem, jak ani nevypíchnout nic nikomu jinému šmytcem sakra, jak to šmytcem bolí, když dostanete přes prsty, protože neposloucháte a konečně, jak si zapamatovat, že se neříká šmytec, ale smyčec. Jauvajs!
No a když tyhle štrapáce nezbytné rozcvičky překonáte, začíná hudební průprava podle Otakara Ševčíka, což jak jsem pochopil, byl pro mladý houslisty něco jako Jan Kámoš Komenský. A podle Ševčíka se učíte hrát nejprve na prázdných strunách. A těm prázdný strunám odpovídají, respektive měly by odpovídat noty na notové osnově. A tady se už konečně dostávám k oněm zásadním disharmoniím hudebního světa mezi tradiční školou státní a školou ševčíkovsky houslovou. Nejtlustší struna se jmenovala Gé, další pak Dé, Á a ta nejtenčí, kerá se nejbolestivěji zařezávala do prstíků, což trochu předbíhám, tak ta byla É. Tedy ještě jednou: GÉ, DÉ, Á, É. A ty noty stejně tak. (Což uznávám, že mohlo být teoreticky ještě horší.) Ale zkrátka ta posloupnost byla úplně jiná než jakou nás učila soudružka ve škole. Zašel jsem tam teda ještě jednou a fakt. Ve škole tvrděj, že Gé i É jsou před A!
Buďto mi teda lže Otakar Ševčík s Turzou, nebo úča a celý základní školství! Turza byl v době socialismu evidentně nedůvěryhodnej už proto, že mluvil německy, italsky a latinsky, učitelce zase nepřidávaly body poznámky, který mi ustavičně i přes napomínání psala do mojí, podtrhávám mojí, žákovský knížky. Zjistit, na který straně je pravda, se mi na rozdíl od Fučíka jen tak nepodařilo. A tak jsem celou druhou čtvrtou třídu melancholicky chřadl s překvapivě zralým filozofickým poznáním, že svět nedává smysl.
Asi po dvou letech pozorování mého hudebního entuziasmu a dvou zlomených smyčcích (vida, ja to jde!) pan učitel Turza naznal, že by mě moh teda pustit k prstokladu, odložil svůj rozjezený chleba se sádlem a mastnými prsty slavnostně obrátil Ševčíka na stránku číslo štyry. A tam to bylo! Těch tónů existovalo mnohem víc než strun na mejch houslích: gé, á, há, a pozor, pak to pokračovalo: cé, dé, é, ef, gé, á, há, cé. Byla to zkrátka posloupnost, která se opakovala, byla v zásadě stejná jako ta, co do nás hustila souška, jen začínala o nějakých pár tónů dříve a končila pozdějc. Můj smysl pro konzistentně bezesporný systém byl konečně uspokojen. Vytahal jsem šipky zabodnuté do Albertových bystrých očiček, jehož podobiznu jsem měl inspirativně přilepenu na skříni svého pokoje a dal logice hudby znova šanci.
Turza nevěřil svým naslouchátkům. Pochopit význam tónu cis, tedy c zvýšeného křížkem mi najednou zabralo jen přibližně dvaatřicet krát méně času než to, že “vysoké é…..é je vysoké...no snaž se... je teda logicky vyšší než á, ne? když je tááákhle vysoké přece”.
Matematika hudby se začala záhy rozvíjet v celé své nádheře. Jelikož interval oktávy odpovídá dvojnásobné frekvenci tónu a tyto tvoří geometrickou řadu, musí mít jeden každý ze dvanácti půltónů frekvenci vyšší o dvanáctou odmocninu kmitočtu nižšího z nich, zjistil jsem.
Jak uspokojivé! A přesto Turza neoblobně trval na zápise tónů prostřednictvím podivných grafických značek s vlaječkama. Ale už mi to nevadilo, neboť jsem věděl, že tam někde nahoře svačí svůj chleba se sádlem skutečný matematický bůh, který dbá o to, aby všechny ty lidské, ševčíkovské, učitelské, hudební, zdánlivě protiřečící si názory, módy uvažování i teorie nakonec zharmonizoval svým všeobjímajícím matematickým smyčcem…
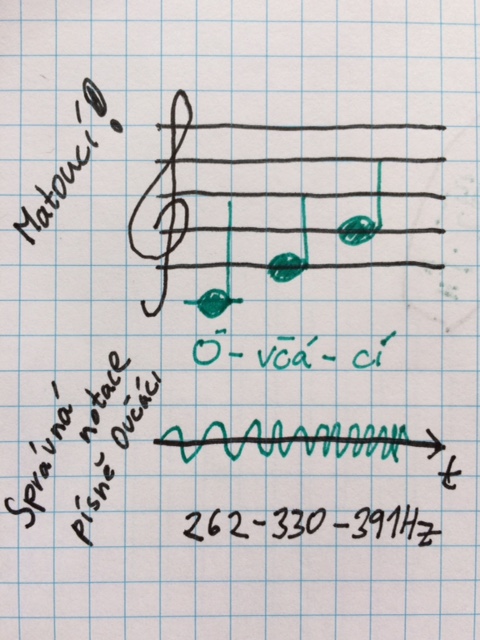
Seriózní pedagogická douška pod čarou, ať těm dětem nepletete hlavy:
Rozechvělá struna vydává tón. Třeba Á. A taková struna kmitne 440 krát za vteřinu. A když ji přesně v půlce podržím prstem, chvěje se už jen ta její půlka, zato dvakrát rychleji, tedy 880 krát za vteřinu. A zní přesně o oktávu výše. A taková oktáva našemu uchu celkem lahodí - můžeme tak zpívat společně s dětma a ladí nám to. A protože to kmitání oktáv jde po dojnásobcích, tvoří sama řada oktáv geometrickou řadu: 110, 220, 440, 880…A oktáva se jí říká proto, že jsme si tuhle vzdálenost rozdělili do osmi nejčastěji broukaných tónů: do, re, mi, fa, sol, la, ti, do! Je jich osm a poslední ladí s prvním. Někdy ale v písničkách, třeba těch smutnejch, chceme občas udělat menší krok než tón. Třeba půltón. A takových půltónů máme do oktávy dvanáct, stejně jako je klapek na klaviatuře od cé do cé, nebo od á do á, některý bílý, některý černý, ale to je stejně jako u lidí, fuk. Je jich dvanáct stejně jako apoštolů. Chceme-li do každé z oktáv vměstnat rovnoměrně dvanáct půltonů, musí platit, že 440 Hz = 220 Hz*q*q*q*q*q*q*q*q*q*q*q*q, tedy 2=q12 (na dvanáctou) a tak je kvocient, kterými musíme násobit výšku tónu, abychom dostali tón o půltonu vyšší, dvanáctou odmocninou ze dvou.
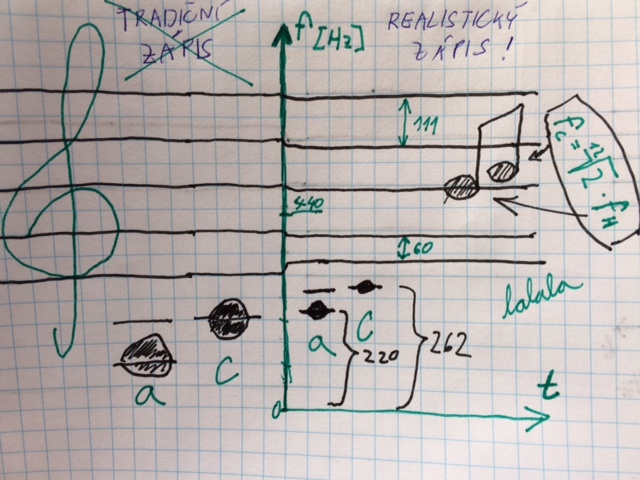
Pro obzvláštně vnímavé čtenáře dodejme, že notová osnova je lehce zkreslující, jelikož naznačuje, že vzdálenosti mezi tóny jsou rozložené lineárně, všechny linky jsou na ní od sebe stejně daleko. To však není pravda; ve fyzikální skutečnosti jsou tyto intervaly rozložené nerovnoměrně -viz obrázek. Tím se však netřeba nechat mást. Koneckonců, výška tónu je pouhá frekvence, kmitočet, a měla by se spíše zobrazovat na ose časové, x-ové, kdežto y-ová osa by spíše než výšce měla odpovídat hlasitosti! Takový zápis by byl konečně čirá, matematická krása...
Přidat komentář